CONTEXT DEL PROJECTE
Després d’haver treballat HTML, CSS i JavaScript als tres primers mesos del curs, els alumnes de 1r de batxillerat tecnològic hem realitzat un treball utilitzant el llenguatge de programació Python.
Aquest projecte ha constat de que cada alumne ha hagut de realitzar i exposar a classe un capítol del llibre “Real-World Python - A Hacker's Guide to Solving Problems with Code” de Lee Vaughan, escollit aleatoriament pel professor.
En el meu cas, com a l'optativa som once i hi havia 12 capítols, em va tocar escollir entre un dels dos últims, que eren els més complets. Primer vaig intentar solucionar els errors del codi del capítol 11, però no em va sortir del tot bé i finalment vaig fer l’últim, el capítol 12, i aquí ho explicaré tot.
¿QUÈ ÉS UNA ANISOTROPIA?
Abans de res, introduiré un concepte important, la isotropia i anisotropia, i ho faré mitjançant l’exemple de l’estudi que va fer una alumna de 2n de la explosió d’una supernova. Deixo l’enllaç al vídeo amb més detall.
(Imatge 1) (Imatge 2)
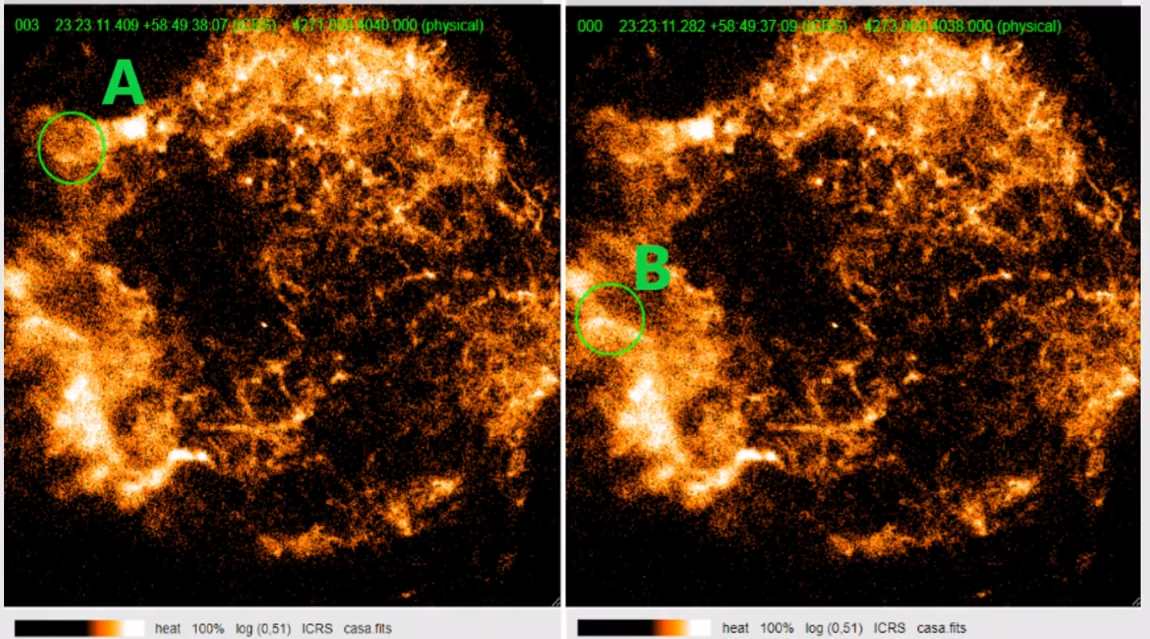
El primer que va fer va ser agafar una supernova, Cassiopeia A, i va definir dos punts, el punt A i B (Imatge 1).
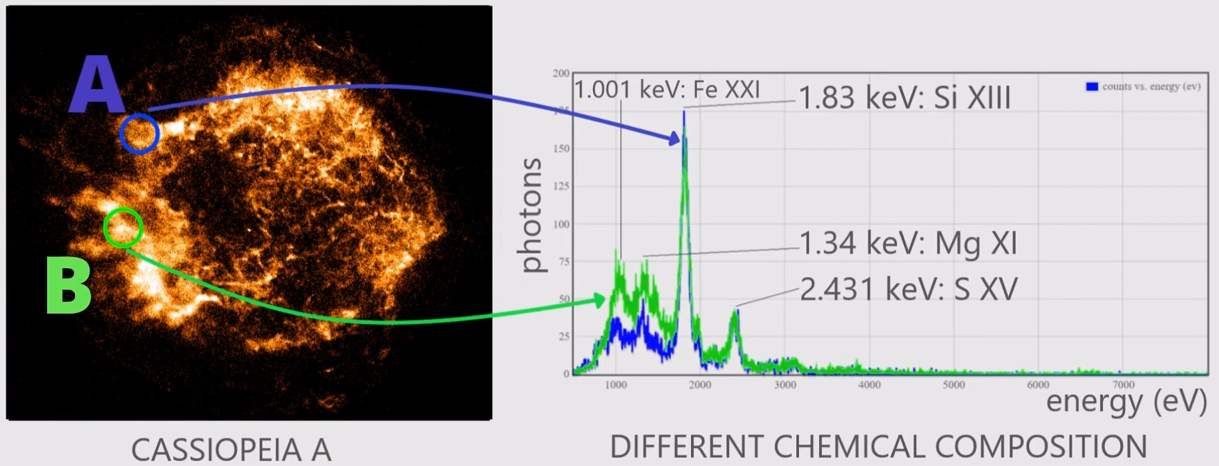
Seguidament amb un espectròmetre d’imatges CCD de raigs X va prendre mesures de l’energia que tenien els dos punts diferentes, la línia blava representant el punt A i la verda, el B, tal i com es pot veure a la Imatge 2. El resultat va ser bastant interessant, ja que el que tothom i el que la ciència pensaria seria que aquesta explosió seria igual en quant a lluminositat, composició química, energia, etc., és a dir, seria isotròpica per a totes les direccions, però no, va resultar que encara que els pics d’energia a la gràfica eren similars, els del punt B eren significativament superiors als del punt A, i fins i tot estaven químicament composades per diferents elements, i de fet a partir d’aquest mètode d’investigació de supernoves és com es
van descobrir molts minerals i es van adonar que una molt petita part de nosaltres també prové d’aquestes. Aquestes diferències entre diverses direccions són les anisotropies.
(Imatge 3)
EXPLICANT ELS CODIS
Un cop introduït el què és una anisotropia, explicaré el capítol 12, titulat “Estem vivint en una simulació d’ordinador?”. Com diu al títol, l’objectiu és identificar una característica d’una simulació per ordinador que pugui ser detectable per qui estan sent simulats (suposant que nosaltres som una simulació). Per cert, abans d’explicar els codis i la relació que tenen amb l’objectiu i les anisotropies, he d’avisar què és un projecte que pot arribar a costar d’entendre i s’ha de prestar atenció al que es llegeix, fins i tot podria considerar-se una mica filosòfic.
Codi 1: pond_sim.py
1- import turtle
2-
3- pond = turtle.Screen()
4- pond.setup(600, 400)
5- pond.bgcolor('light blue')
6- pond.title("L'estanc de Yertle")
7-
8- mud = turtle.Turtle('circle')
9- mud.shapesize(stretch_wid=5, stretch_len=5, outline=None)
10- mud.pencolor('tan')
11- mud.fillcolor('tan')
12-
13- SIDE = 80
14- ANGLE = 90
15- log = turtle.Turtle()
16- log.hideturtle()
17- log.pencolor('peru')
18- log.fillcolor('peru')
19- log.speed(0)
20- log.penup()
21- log.setpos(215, -30)
22- log.lt(45) # Rotació en graus.
23- log.begin_fill()
24- for _ in range(2):
25- log.fd(SIDE)
26- log.lt(ANGLE)
27- log.fd(SIDE / 4)
28- log.lt(ANGLE)
29- log.end_fill()
30-
31- knot = turtle.Turtle()
32- knot.hideturtle()
33- knot.speed(0)
34- knot.penup()
35- knot.setpos(245, 5)
36- knot.begin_fill()
37- knot.circle(5)
38- knot.end_fill()
39-
40- yertle = turtle.Turtle('turtle')
41- yertle.color('green')
42- yertle.speed(1)
43- yertle.fd(200)
44- yertle.lt(180)
45- yertle.fd(200)
46- yertle.rt(176)
47- yertle.fd(205)
Execució del codi:
(Imatge 4)
Primerament, s’importa la biblioteca turtle, la qual es bastant fàcil d’utilitzar i fa les coses més senzilles.
De la línia 3-6 crea l’aigua d’un estanc i posa el títol de la finestra.
De la 8-11 dibuixa un cercle que simula una illa de fang on es troba Yertle, la tortuga protagonista.
Després, defineix dues constants a les línies 13 i 14 i crea un tronc de la 15-29, al que anirà Yertle nedant des de l’illa quan s’executi el codi.
De la 31-39 fa un forat purament decoratiu al tronc.
I finalment de la línia 40-41 crea a la tortuga Yertle i de la 42 a la 47 estableix el moviment que farà indicant els angles en graus i la seva velocitat, que és bàsicament de l’illa al tronc, torna a l’illa, agafa un cert angle i es dirigeix al tronc, on s’atura.
La importància d’aquesta tonteria està en que la línia de dalt és anisotròpica i per aquest motiu els píxels fan ziga-zagues i la línia es veu amb forma de escala (Imatge 5), mentre que la de baix, la isotròpica, és totalment recta.
(Imatge 5) (Imatge 6) (Imatge 7)
Això es pot aplicar a la realitat, ja que la comparació més clara seria els àtoms o fins i tot partícules subatòmiques amb els píxels.
També hem de saber que els píxels formen un patró ortogonal (Imatge 6), i si sobre aquest patró dibuixem les dues línies del traçat de Yertle quedarien com a la Imatge 7. I aquí és quan treiem una de les moltes conclusions importants, que és que aplicant el teorema de pitàgores, si la línia isotròpica mesura 1, la anisotròpica mesura més de 1, ja que el quadrat de la hipotenusa (línia inclinada) és més gran que el de qualsevol dels dos catets (línia recta), llavors la línia anisotròpica té més energia que la isotròpica.
Codi 2: line_compare.py
1- from time import perf_counter
2- import statistics
3- import turtle
4-
5- turtle.setup(1200, 600)
6- screen = turtle.Screen()
7-
8- ANGLES = (0, 3.695220532)
9- NUM_RUNS = 20
10- SPEED = 0
11-
12- for angle in ANGLES:
13- times = []
14- for _ in range(NUM_RUNS):
15- line = turtle.Turtle()
16- line.speed(SPEED)
17- line.hideturtle()
18- line.penup()
19- line.lt(angle)
20- line.setpos(-470, 0)
21- line.pendown()
22- line.showturtle()
23- start_time = perf_counter()
24- line.fd(962)
25- end_time = perf_counter()
26- times.append(end_time - start_time)
27-
28- line_ave = statistics.mean(times)
29- print("Angle {} degrees: average time for {} runs at speed {} = {:.5f}"
30- .format(angle, NUM_RUNS, SPEED, line_ave))
Execució del codi:
(Imatge 8)
S’importen les biblioteques perf_counter (de time), per mesurar temps amb alta precisió, statistics per a fer càlculs estadístics i matemàtics, que la farem servir juntament amb perf_counter per calcular el temps de computació respecte l’angle de cada línia i també turtle, encara que en aquest codi només es fa servir per donar un cert tamany a la finestra (línia 5 i 6) i crear les línies.
A les línies 8-10 es determinen les tres constants base amb les que funciona el codi, ANGLES fa que la primera línia sigui recta i la segona tingui un de 3.695220532°, NUM-RUNS indica la quantitat d’execucions, en aquest cas 20, i SPEED és la velocitat amb què es creen les línies, ara està a 0, que és la velocitat màxima possible.
De la línia 12-26 es fa que les 20 execucions de cada línia es creïn en bucle, una seguida de l’altra, i a la línia 26 el que fa el mètode times.append(end_time - start_time) és anar afegint la variació de temps a l’altra, va sumant el temps de les execucions a l’objecte times.
Finalment, a la 28 es defineix la variable line_ave fent la mitjana dels temps amb el mètode mean i a la 29 i 30 s’indica que s’escrigui un missatge (Imatge 9) dient a cada línia la mitjana de temps en segons per crear-se cadascuna segons les 20 execucions i la velocitat predeterminada. Aquest temps es fa que tingui 5 decimals amb l’expressió {:.5f}, que significa (en aquest cas 5) floating numbers.
(Imatge 9)
Una altra conclusió és que segons l’estadística, la línia anisotròpica té més temps de computació que la línia isotròpica, i això vol dir que segurament hi hagi alguna forma de manipular aquests temps i fer alguna bretxa dimensional, tal com ocorre en un episodi de Rick i Morty, però això encara s’està investigant i estem esperant per a una resposta científicament vàlida.